Using structural models
|
Subsurface fracture problems are commonly attacked with statistical methods and
several sections of this website (Part 8) are about fracture and orientation
statistics. Section 1.3 is about deterministic prediction of the spatial
location and intensity of fracturing. This discussion explains how these two
very different approaches fit together.
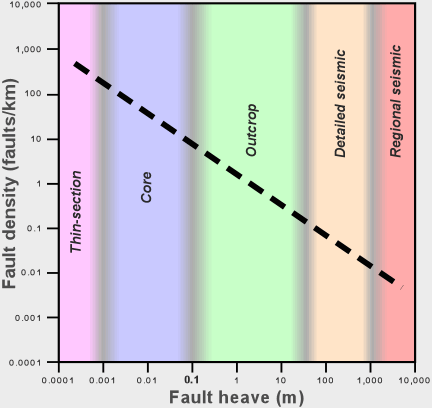
An example of a statistical method. Since 1990 a number of studies in many different geologic environments have shown that when fault size is plotted against fault density (surface area/unit volume) on a log-log plot, the result is a straight line, as shown in Figure 1. The slope and intercepts of the line vary, but the line is always straight. Saying that the fault population is "fractal" is just another way of saying the same thing. |
Figure 1
|
Joint populations appear to behave similarly and there are sound mechanical reasons for
this relationship. The relationship appears to be constant from the scale of regional
seismic surveys to the scale of individual grains within the rock. The beauty of this
relationship is that because it is linear, the entire population can be characterized
completely by observing it at any scale.
Statistics vs. Determinism. The previous discussion leads to obvious questions like: Why bother doing careful geology if I can know everything about the entire fault population all the way down to the grain scale just by counting faults in my seismic line/volume and calculating this groovy statistic?To which there are two answers that depend on this key point: If the data are apples, then a statistic is applesauce.The answers are:
Devotees of fault-scaling methods will argue that answer #2 is incorrect because the population will have the same fractal dimension regardless of where you sample it. Even if they are right, answer #1 still holds. In other words, we don't want to know simply that there are heavily fractured areas out there somewhere, we want know where they are, how big each one is, and how heavily fractured they are so that we can drill into, avoid, or correctly model them depending on our needs. In short: It's a matter of scale. The best approach for analyzing reservoirs is to use deterministic geologic methods to classify/specify the fracture character and distribution down to the smallest practical scale and then work stochastically at and below that scale. If time or data restrictions force us to work stochastically at an undesirably large scale we can still compute useful parameters, but the computed results and especially the final geological model(s) will not reflect reality as accurately as they would if the data were subdivided in a geologically meaningful way prior to statistical analysis and simulation. Conclusion: Deterministic geology should be used whenever practical to define reservoir volumes prior to statistical analysis. |
CONTENTS
|
When is a rock mass deformed enough to need quantitative structural analysis? |
| Section 1.3 is concerned with the general subject of using quantitative structural methods to define rock volumes that fractured during folding. If the rocks become fractured locally by folding then they must have started off as a homogeneously fractured or unfractured mass. Many oil fields, and many fractured reservoirs, occur in flat-lying, relatively undeformed rocks. How deformed do the rocks have to be before we need to treat them as heterogeneously fractured and use quantitative structural methods? To answer this question let's consider how a rock mass with a homogeneous fault population converts into a heterogenous one by continued fault movement. Figures 2 and 3 show some of the famous hoodoos at Bryce Canyon National Monument, Utah, U.S.A.. The leading edge of a now inactive fold-thrust belt lies several miles to the left of the area shown in the photos. During propagation of the thrust belt, the rocks were deeply buried and were mechanically continuous with the fold-thrust belt. Erosion removed the overlying rock after the thrust belt became inactive. Bedding in the hoodooos is horizontal so it has not been disturbed by large-scale deformation. Two conjugate sets of small thrust faults with very little slip are readily visible. One set dips 30° to the left, one set dips 30° to the right, and the dip-azimuths of both sets are approximately perpendicular to the fold-thrust belt. The faults formed during propagation of the thrust belt and represent the earliest stage of failure of the strata (___, 19__). Even at this stage of development, slight fault-related folding of the strata is already evident on some of the larger faults. Had the fold-thrust belt continued to propagate, some of these faults would have grown and eventually would have produced folds like the ones described in Page 1.3.3. | ||

|
Notice that faults are present at all scales. The faults must be quite small because
both terminations of many of them are visible and because many prominent faults do not
visibly offset or fold bedding. Folks with patience and/or a fast internet connection should download high-resolution versions of these photos from the NaturalFractures.com album at PhotoPoint and look at these pervasive fault sets in detail. Select the options View then View this photo full-size. |

|
The planarity of the faults and the presence of two well-defined, contemporaneous groups suggests that the area shown in Figures 1.3.1-2 and 3 can be treated as a homogeneously deformed volume of rock. The fracture density should be fairly uniform because the fracture density was controlled by random nucleation of faults throughout the rock mass and the rocks are homogeneous, bedding is consistently horizontal and the rocks were probably stressed fairly uniformly because they are are well forward of the leading edge of the fold-thrust belt. If this area was an oilfield then we would treat it as a statistically homogeneous volume. Now let's imagine that the faults had continued to move so that fault-bend folds (Page 1.3.3) started to form. At what stage of fold development would we have to take localized deformation into account? Virtually any degree of fault-related folding is significant because the kink bands that are fault-bend folds can propagate indefinitely and even completely through the stratigraphic section and even a small increment of movement can form narrow, but extensive, fracture zones (Figures __ and __). may have formed in this manner. Unfortunately, we can't use structural models to predict fractured areas if there isn't enough structural relief to detect in seismic data and we don't have other surface or subsurface structural data. Conclusion. Kinematic structural modeling should be used to define structural domains whenever detectable fault-related fold structures can be resolved with available data. |
CONTENTS
|
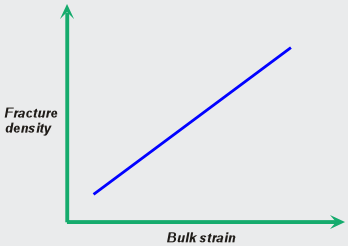
Bulk strain does not predict fracture type or density |
The pages in section 1.3 show how quantitative structural models are used to predict
the bulk rock strain caused by various types of folding from accurate representations of
subsurface structure. Since modern seismic data is an excellent source of subsurface
structural information, it should be possible to develop a relationship between strain and
fracture denisty (fracture surface area/unit volume) or other fracture system properties,
as shown in Figure 4. With such relationships, we should be able to predict
fracture system properties in advance of drilling and use this information to optimize
exploration and development wells and to build accurate geologic and engineering models
of a reservoir. Unfortunately, we need more information than just the bulk strain to
accomplish these goals.
|
Figure 4
|
|
Relationships between strain and fracture properties must be
developed and calibrated for an area of interest using subseismic-scale data
because strain predictions from structural models are useful for predicting
the spatial location of fracturing,
but say nothing about important fracture system properties such as the number, type,
orientation, density, size distribution, permeability, porosity and stratigraphic heave
distribution (in the case of faults) of each fracture set. Bulk strain information alone
cannot predict fracture properties because a given bulk strain can be accommodated by
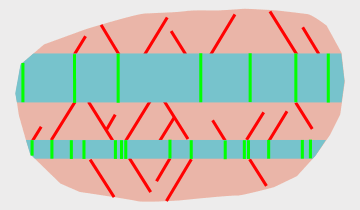
fracturing in an infinite number of ways. Figure 5 shows how a fixed amount of extension
of a single bed can be accomplished by densities of either joints or faults.
| | |||
Figure 5
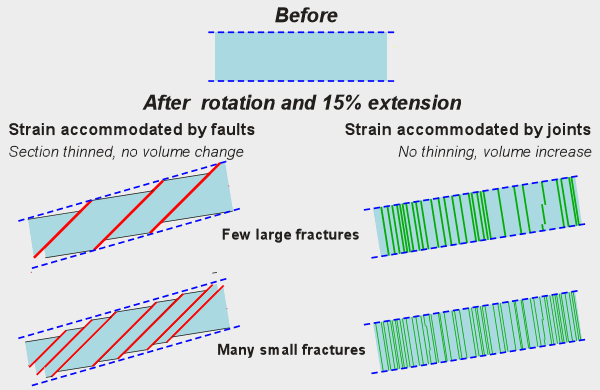
|
Conclusion: Bulk strain alone is not a predictor of fracture system properties. |
CONTENTS
|
Joints or faults? It matters. Different
fracture types
form in different orientations relative to the principal stresses, have different
termination relationships, fluid-flow behavior, relationships to other types of
fractures and geologic structures, and size/shape distributions. A method of
predicting fracture type without subseismic-scale data would clearly be useful. We
know that knowledge of the bulk strain alone is
insufficient to determine fracture type, but perhaps bulk strain data combined with
other information would be sufficient to theoretically predict fracture type. We'll
discuss fracture-type prediction in terms of joints vs. faults because these are the
two most common fracture types and have very different fluid-flow properties.
The left and right sides of Figure 5 clearly would exhibit different fluid-flow behavior. Note that idealized, planar faults accomodate strain without producing any porosity or permeability but joints increase the porosity and permeability of the rock mass. In nature faults can be barriers to fluid flow, can be highly permeable or anything in-between. | ||
| Figure 6: Fracture type and lithology. Individual lithologies often fracture differently, and even interbedded litholgies with different mechanical properties may develop different types of fractures as illustrated in Figure 5. When interbedded lithologies develop different types of fractures, the amount of strain is equal in each lithology (Gross 199_). Note that permeable joints may provide no communication perpendicular to bedding if they are only developed in one lithology in an interbedded sequence of two or more lithologies. |
|
|
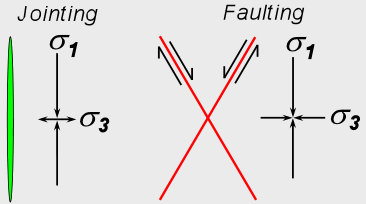
| Figure 7: Joints or faults? The type of fractures that form in a rock are a function of the mechanical properties of rock (such as strength) and the effective stresses in the rock during deformation. Joints form when the minimum principal effective stress is tensile. Faults form when all of the effective stresses are compressive and there is a sufficiently large difference between the maximum and minimum principal stresses. Figure 6 shows the relative magnitudes of the stresses during jointing and faulting. |
|
|
Stress state. The stress
state of a rock mass is described by the orientations and magnitudes
of all three principal effective stresses. The effective stress state is a
function of three factors:
OK. So how do we develop an accurate understanding of subsurface fracture systems? We do this by: |
||
CONTENTS
|
Wildcat drilling. Wildcats should be drilled in structural domains that are expected to be more heavily fractured, such as domain D3 in Figure 6 or the transversely extended domain shown in Figures 8 and 9. Exploration and delineation drilling. Exploration and delineation drilling should attempt to sample each structural domain prior to development drilling. Reservoir characterization. Structural localization of fracturing has two critical implications for fractured reservoir characterization:
Reservoir simulation. Numerical reservoir simulators use three-dimensional models of subsurface fluid-flow and fluid-storage properties to calculate reserves, reservoir performance, plan development and enhanced-recovery strategies, and other critical tasks. Fractured reservoir simulators must incorporate the effects of fractures on rock mass fluid-flow properties, which presents a problem: Subsurface fracture networks are characterized primarily from wellbore data, but wellbores provide only tiny samples of the reservoir. Structural models of the reservoir provide a way to extrapolate wellbore data throughout the reservoir volume. Fracture characterizations should be extrapolated throughout and only within the structural domain that was the source of data for the characterization. Structural models and seismic data. Seismic velocities and anisotropy are often used as indicators of fracture properties. Unfortunately, seismic data alone are not adequate to characterize reservoir fracturing because fracture systems have many more variables than the complete seismic velocity tensor. However, sesimic data are extremely valuable when used to leverage, test/corroborate, or extend other data sets. In the context of quantitative structural models, seismic information has the potential to delineate fracture domains directly and may indicate the relative intensity of fracturing in each structural domain. The limitation is that that fracture properties such as the number, density (surface area/unit volume), size distribution, and fracture-derived permeability cannot be predicted from seismic data. |
CONTENTS
Copyright © 2000 - 2017 • Alfred Lacazette • All Rights Reserved