Natural Fractures

Extensional fault-bend folding:
Implications for localized fracturing

Contents

Introduction
FLATTENING BENDS: THEORY
Initial state
Solving the room problem by void formation
Solving the room problem by folding
The Coulomb shear model
Quantitative relationships
Folding requires extensional strain
Slip and throw change across a flattening bend
Qualitative predictions
FLATTENING BENDS: EXAMPLES
Example: Outcrop-scale void formation and folding, Eastern Utah, U.S.A.
Example: Outcrop-scale folding, Eastern Utah, U.S.A.
Example: Mara Field, Venezuela
STEEPENING BENDS: THEORY
Initial state
The room problem
Solving the room problem: Extension or shortening?
Slip and throw change across a steepening bend
COMPLEXITIES
Multiple fault bends and 3-dimensional folding
Example: Steepening bend and transport-parallel fault bend, Arches National Monument, Utah, U.S.A.
Systems of extensional faults

Introduction

This material in this section is of direct interest to people working on one or more of the following problems:

Fault seal.
Reservoir compartmentalization or communication by sealing or leaking faults.
Reservoir compartmentalization or communication controlled by juxtaposition of permeable or impermeable beds across a fault.
Any problem in reservoirs with permeable fractures, from wildcatting through reservoir simulation and secondary recovery.
Any geological problem in extended terranes.
Reservoir modeling.

This section covers:

The process of folding at bends of extensional (normal) faults.
How this type of folding produces extensional strain.
How the strain magnitude can be calculated directly from seismic data.
How the strain magnitude is a predictor of fracture strain.

Background. This section assumes that you have read the introduction to Section 1.3 and are familiar with:

Natural fracture nomenclature.

Fracture orientations relative to the orientations of the principal stresses.

Regional fracture orientations.

The discussion in this section is based on a conceptual model of extensional fault-bend folding described in:

H. Xiao & J. Suppe (1991) The origin of rollover: American Association of Petroleum Geologists Bulletin: v. 76, no. 4 (April), p. 509-529..

Background material for non-geologists

CONTENTS

	Flattening bend: Initial state
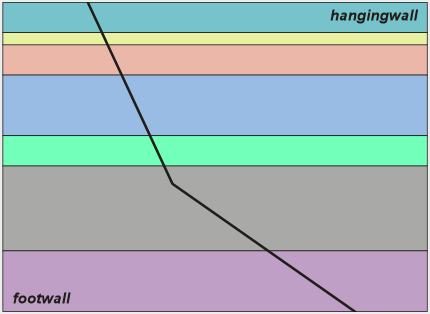
	When faults form, they often develop bends, or changes in orientation. This diagram shows an example of a normal fault with a flattening bend prior to the development of significant displacement along the fault.

Figure 1.

CONTENTS

	Solving the room problem by void formation
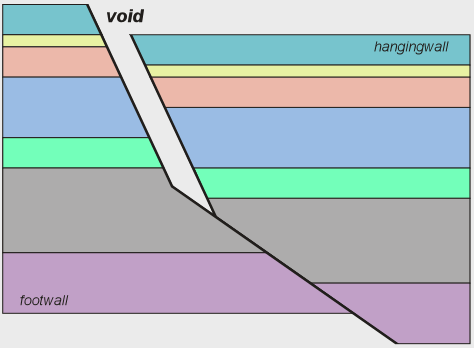
	If rocks were sufficiently strong, then continued fault movement would open a void.

Figure 2.

CONTENTS

Solving the room problem by folding

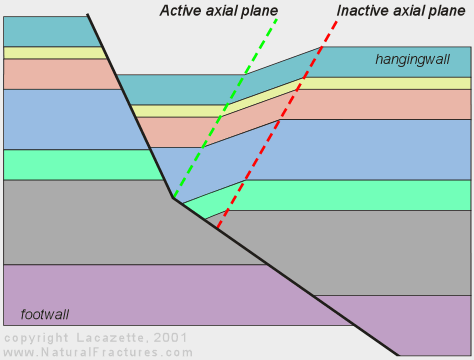
In the earth, rocks must deform to fill the void as the hangingwall block moves past the fault bend. This drawing shows how rocks fold to accomodate this room problem. Key points:

The inactive axial plane moves with the hangingwall block.
The active axial plane is pinned to the fault bend and remains stationary relative to the footwall block.
The rocks fold continuously as they move through the active axial plane.
The rocks can fold by one or more of any possible deformation mechanism, including grain sliding and minor faulting.

Figure 3.

CONTENTS

The Coulomb shear model

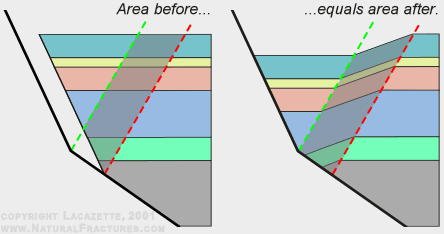
The Coulomb shear model. The drawings on this page are based on the model of Xiao and Suppe (1991). In this model:

Extension is accomplished by Coulomb shear (bulk frictional slip, like in a pile of sand) NOT by flexural-slip of bedding (like bending a deck of cards).

Consequently, this model is applied in exactly the same manner when analyzing basement rocks, massive sedimentary units, thinly layered sedimentary rocks or unconsolidated sediments because bedding is passive during Coulomb shear.

The dip-angle of the fold axial planes is equal to the Coulomb shear-angle of the deformed rocks or unconsolidated sediments. The dip-angle is therefore fixed and is unrelated to the orientation of the fault segments on either side of the bend. Note that axial planes can be reoriented by later deformation.

Material conservation requires that the cross-sectional area of the extended fold panel remains constant, in 2-dimensional models. In three dimensions volume is conserved.

Figure 4.

CONTENTS

	Quantitative relationships

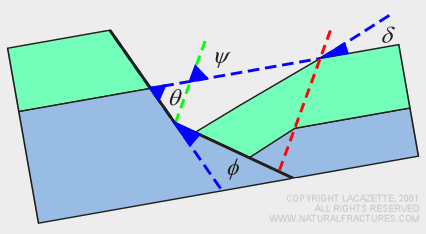
	The Coulomb shear model provides a quantitative relationship between fold shape and fault shape. Diagrams in this document show folding of flat-lying strata for simplicity and clarity. However such folds can form in strata that are already dipping or in unstratified rocks. This equation relating fold shape to fault shape is applicable under general conditions.

Figure 5.

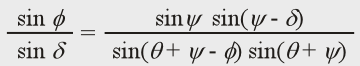
CONTENTS

Folding requires extensional strain

Stratigraphic length L1 must extend to length L2 in the folded panel. The Coulomb shear model makes specific, quantitative predictions about rock strain. Good quality seismic data often resolves the fault and bedding orientations well enough to predict the amount of strain in the folded panel. Regardless of whether or not strain can be computed from seismic data, fold panels of this type must be areas of extensional strain.

Figure 6.

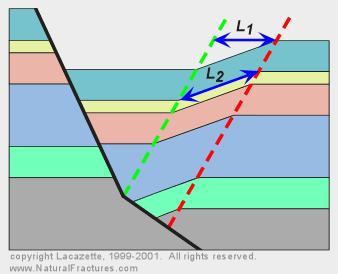
Equation 2.

CONTENTS

Slip and throw change across the fault bend

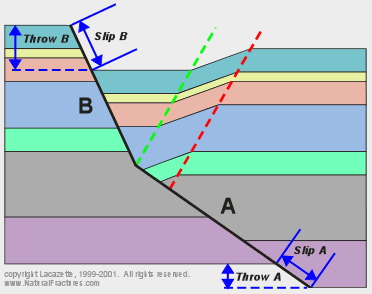
The Coulomb shear model makes specific, quantitative predictions about relative slip magnitudes/rates, and subsidence amounts/rates for each fault segment. In this example, the slip on segment B is 15% greater than the slip on segment A and stratigraphic throw across segment B is 88% greater than across segment A. Consequently, during fault movement the slip rate must have been correspondingly faster on segment B as was the subsidence rate above segment B. The variations in slip rate/amount may be an important control on the size and damage intensity of the fault damage zone.
Compare with a steepening bend.

Figure 7.

CONTENTS

	Qualitative predictions
	If folding-related strain is accommodated by brittle fracturing, then we can predict where fractures are developed with simple structural models.

Figure 8.

CONTENTS

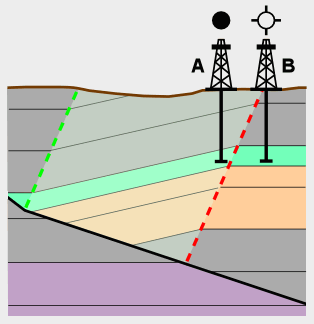
Example: Outcrop-scale void filling and folding, Eastern Utah, U.S.A.

Figure 9 shows the hangingwall block of an extensional fault-bend fold above a flattening bend. The passive limb (where the human is pointing) is weakly jointed. The relatively short extended limb (center right) is cut by normal faults and some joints. The homogeneous mass on the far right is a mud diapir that prevented collapse and folding of the hangingwall by intruding the void as it developed. The fault surface is beyond the right edge of the photo. Compare with Figure 2). Fractures in the hangingwall strike parallel to the fault indicating that transport-perpendicular folding was dominant.

Figure 9.

CONTENTS

	Example: Outcrop-scale folding, Eastern Utah, U.S.A.
	Extensional fault-bend folding due to a flattening bend in a normal fault.

Figure 10a.

Few fractures are present in the footwall block and to the left of the axial plane that divides the passive limb from the extended limb.The red rectangle shows the location of Figure 10B, which is in the extended fold panel.

Figure 10b.

Heavily fractured rock in the extended limb of the fold. Note that extensional strain was accommodated by both normal faulting and jointing.

CONTENTS

Example: Mara Field, Venezuela

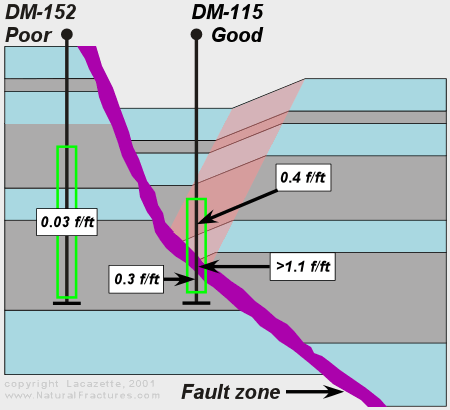
Example of fracturing during extensional fault-bend folding, Mara field, Venezuela (Carmona et al, 1997). Schematic cross-section of a late extensional fault on the flank of the main anticline showing the relative structural positions of two wells. The green rectangles show the depth ranges of the image logs in the two wells. Fracture density (fracture surface area/unit volume) was calculated from fracture data measured in image logs by the method of Lacazette (1991). The computed fracture densities demonstrate the relationship between fracturing and extensional folding. Fracture density is clearly correlated with production. The highest fracture densities were found in the fault zone, and fracture density steadily declines downwards from the fault zone itself. The bottom of the image log in the DM-115 is in the damage zone below the fault zone, so the fracture density at the bottom of the well is still above the values measured in the DM-152.

Figure 9. This is a supplementary figure to Carmona et al, 1997.

CONTENTS

	Steepening bend: Initial state
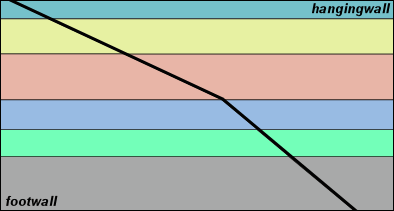
	Faults also develop steepening bends. Deformation at a steepening bend can be treated with the same Coulomb shear model and equations previously discussed for flattening bends.

Figure 12.

CONTENTS

	The room problem
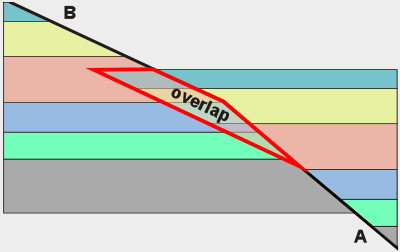
	In this case slip along segment A appears to require the hangingwall block above segment B to penetrate the footwall block, which is impossible if material is conserved.

Figure 13.

CONTENTS

	Solving the room problem: Extension or shortening?
	Both extension (Figure 14) and shortening (Figure 15) are geometrically acceptable solutions to the room problem. However, only extensional folding is compatible with extensional stress because shortening requires the wrong shear-sense at the active axial plane. Folding of the type depicted in Figure 15 indicates wrench faulting and/or polyphase deformation.
	Figure 14	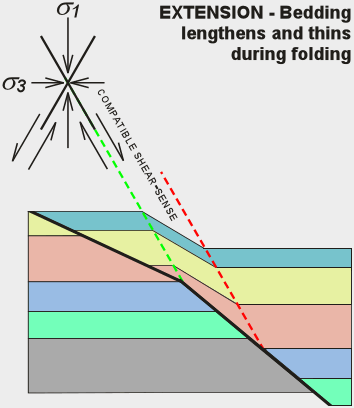Figure 15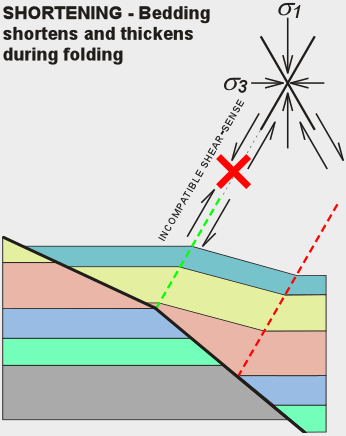

CONTENTS

Slip and throw change across a steepening bend

As in the case of a flattening bend, the Coulomb shear model makes specific, quantitative predictions about relative slip magnitudes/rates, and subsidence amounts/rates for each fault segment. Again, both fault slip and stratigraphic throw change across the fault bend. In this example, the slip on segment B is 68% of the slip on segment A and stratigraphic throw across segment B is 45% of that across segment A. During fault movement, the slip rate is correspondingly slower on segment B as is the subsidence rate above segment B. Again, the variations in slip rate/amount may be an important control on the size and damage intensity of the fault damage zone.

Figure 16.

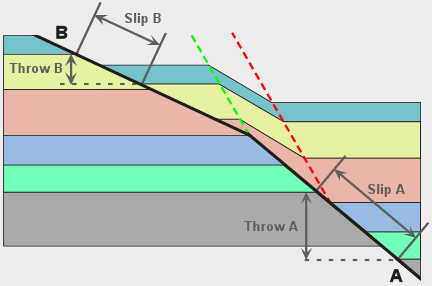
Steepening and flattening bends may appear to be simple geometric opposites of each other, but there is a critical difference: At at steepening bend the friction on the upper fault segment is higher than on the lower fault segment but the reverse is true on a flattening bend. Because of this difference, the hangingwall above a steepening bend tends to detach causing the fault to steepen or straighten but the hangingwall above a flattening bend tends to move with the rest of the block and undergo extensional folding as it collapses to fill the void.

CONTENTS

	Multiple fault bends and 3-dimensional folding
	Figure 16 illustrates two important complexities that all real faults exhibit: Multiple fault bends and fault bends parallel to the transport direction.

Figure 17.

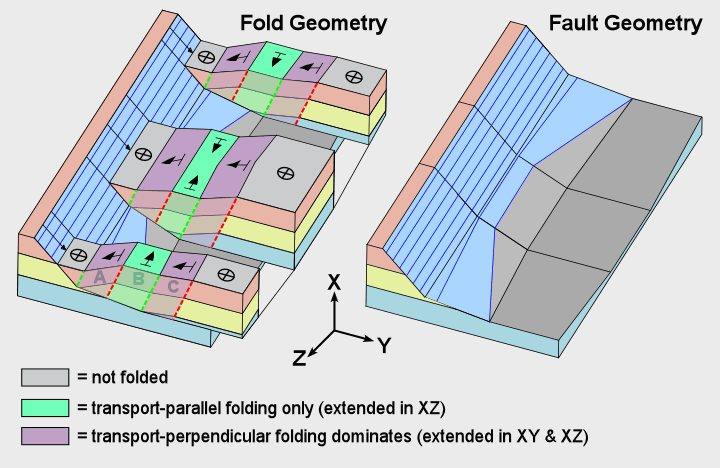
The hangingwall of a fault with multiple bends can experience multiple distinct episodes of deformation in a single continuous deformation, as shown in Figure 16. Fold panels A and C are folded about an axis perpendicular to the transport direction, but A and C are strained by different amounts because the angles of the transport-perpendicular fault bends that produce each panel are different. All three fold panels are folded about an axis parallel to the transport direction, but fold panel B suffers transport-parallel folding only. As a package of rock passes from A to B deformation changes from a combination of transport-perpendular and transport-parallel folding to transport-parallel folding only. Rocks passing from B to C also undergo a second deformation. The hangingwall block shown in Figure 16 will contain at least 12 distinct structural domains, as listed in Table 1:

Table 1.

INITIAL

FINAL

LEFT SIDE	RIGHT SIDE
1. Undeformed rocks above panel A.
2. Folded in A.	3. Folded in A.
4. Folded in A & B.	5. Folded in A & B.
6. Folded in B only.	7. Folded in B only.
8. Folded in B & C.	9. Folded in B & C.
10. Folded in C only.	11. Folded in C only.
12. Undeformed rocks below panel C.

LEFT SIDE	RIGHT SIDE
1. Undeformed rocks above panel A.
2. Folded in A.	3. Folded in A.
4. Folded in A & B.	5. Folded in A & B.
6. Folded in A, B & C.	7. Folded in A, B & C.
8. Folded in B & C.	9. Folded in B & C.
10. Folded in C only.	11. Folded in C only.
12. Undeformed rocks below panel C.

The number of folded panels is doubled because the left and right sides of the hangingwall block are mirror images of each other so the orientations of the strains are different so that the fractures on each side will have different orientations. Initial and Final refer to the periods before and after enough extension occurs for rocks from panel A to become part of panel C.

Quantitative structural analysis can divide geologic structures into domains with homogeneous deformational histories. Quantitative fracture data at one location in a domain can be extrapolated throughout the domain, so that a fracture model for an entire field can be estimated in three dimensions.

CONTENTS

Example: Steepening bend and transport-parallel fault bend, Arches National Monument, Utah, U.S.A.

This example shows extensional fault-bend folding parallel and perpendicular to the transport direction above both flattening and steepening bends in a thick sandstone formation. The red shale that overlies the sandstone has been eroded off but the sandstone has hardly eroded at all so that we can see the complete 3-D shape of the structure.
Fracture cognoscenti will recognize this as one of Marco Antonellini's PhD field areas, but this crude interpretation is my own so please don't blame Marco for it.

Figure 18 (136kb)

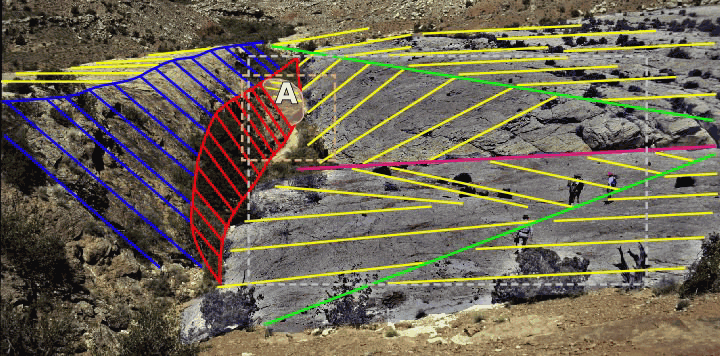
The sandstone surface to the right of the fault was digitally enhanced to make fractures more visible.
Green lines: Fold hinges.
Magenta line: Trace of a tear fault.
Yellow: Dip on the surface of the sandstone layer.
Blue: Dip on shallow parts of the fault surface.
Red: Dip on a steep patch of the fault.
Click in the rectangles to bring up detailed photos of these areas in a new browser window.
Small rectangle (59kb): Remnant (A) of the hangingwall above the steep fault patch. Note that bedding in the block dips shallowly to the right unlike bedding in the footwall and in the passive (non-extended) domain in the hangingwall.
Large rectangle (199kb): Unannotated, enhanced detail showing fracturing in the extended fold limbs. Note the orientations and style of fractures in the lower left corner.

Notice that:

The stream valley at the base of the fault outcrop is wide in the vicinity of the steep patch.

Vertical, roughly fault-parallel fractures predominate in the valley walls.

If you have read this entire page, then you should be able to explain, or at least speculate about:

The shape and dip-directions of the left-dipping fold limbs, their geometric relationship to the tear fault, the orientation of the tear fault, and why the fault is centered on the steep patch.
1. Do these features tell us about the shape of the fault below the ground surface?
2. Is there another fault bend underground? What kind?
3. Could you determine the depth and angle of the bend if you had quantitative data for this structure?
4. What happens to the bend along the strike of the fault? Is this reflected in the shape of the fold in the hangingwall?
The orientations of fractures in the hangingwall block.

Comparing the dip-angles, dip-directions and elevations of the top of the sandstone in the footwall and in the passive (non-extended) fold limb in the hangingwall indicates that there wasn't much slip on the fault and that a relatively unfolded, flat-dipping structural domain should be present where the valley is. The surface of the hangingwall fragment (A in Figure 18) is continuous with the surface of the extended limb and appears to represent a piece of the rock from this domain. With all this in mind:

What happened to the rest of the rocks in this hangingwall domain and why did it happen?
Why didn't the hangingwall fragment (A) suffer the same fate as the rest of the rocks in its domain?
Does your answer to the previous question indicate a way to improve the interpretation sketched on Figure 18? Look at the detailed photos. Did I make a mistake with the annotation in Figure 18?

Please ask questions, discuss or rant if you are so inclined.

Folks with patience and/or a fast internet connection can download an unannotated, unenhanced, high-resolution version of Figure 18 from the NaturalFractures.com album at PhotoPoint and look at the fracturing in detail. Follow the link then select the options View then View this photo full-size.

CONTENTS

	Continue to page 1.3.3: Fracturing during contractional fault bend folding